Summary

• Describes models for representing belief dynamics in a social network using a simple discrete-spin statistical physics framework
• Demonstrates how the parameters of these models can be determined from empirical data
• Presents the predictive value of the models using real-world studies of belief change in social networks

Belief models

The framework for these models describes a collection of autonomous "agents", a set of possible states for each agent, and the dynamics by which an agent updates their state over time

Ising model

Each agent's belief at time $t$ can be represented by an Ising spin $\sigma_i(t) = \pm 1$; so, each agent can only have one state (agree/disagree, Democrat/Republican, etc.). The "satisfaction" of agent $i$ can be represented by a Hamiltonian-like function $\mathcal{H}_i$; the lower the value of $\mathcal{H}_i$, the higher the satisfaction, and vice-versa:

$$\mathcal{H}_i=-h_i^{\text{eff}}\sigma_i=-h_i^{\text{soc}}\sigma_i-h_i\sigma_i$$

$h_i^{\text{eff}}$ describes the total effective field (Note: like influence) on a node, including its internal field, $h_i$, and "social field", $h_i^\text{soc}$

Initial conditions

The spin value, $\sigma_i$ for each node $i$ must be set to some initial value; it's often approximated using survey results or inferring them from secondary data sources, like social media behaviors

Social interaction term

The social interaction term, $h_i^\text{soc}$, describes the "social field", or how the beliefs of node i's neighbors influence the belief of node i. The paper considers three social interaction rules:

1. Voter model (unbiased random copying): each node chooses a single neighbor, uniformly at random, and adopts that neighbor's belief state
2. Majority rule model (conformism): each node adopts the majority belief state amongst its neighbors
3. Expert rule model: each node adopts the belief state of one specific neighbor considered to be an expert, or somehow favored, on the issue

Internal field term

The internal field term, $h_i$ describes how likely a belief is to be accepted by node $i$. The paper argues that the relative importance of "intrinsic predispositions vs. social influence" differs per individual, so they introduce $0 \leq \alpha \leq 1$, which describes the relative weight between these two factors:

$$\mathcal{H}_i=-\alpha \sigma_i h_i^{\text{soc}} - (1-\alpha)h_i\sigma_i$$

Note: I'm not really sure what the basis is behind the introduction of $\alpha$, and why it's zero-sum.

Network structure

In order to test the dynamics of beliefs within a social network, the network needs a structure (the total number of nodes, and the edges between each node). The paper uses five different network structures (below).

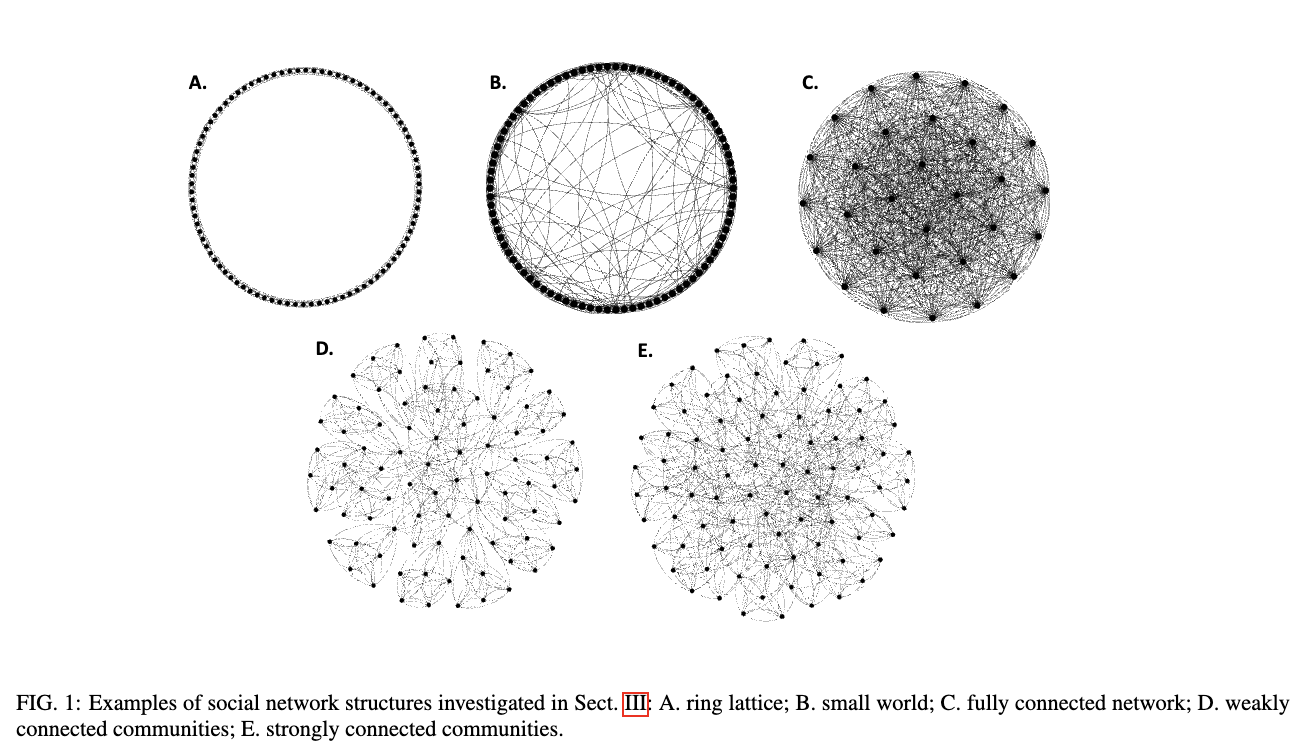
The ring lattice and fully connected graph approximate some real-world networks (Note: really?) and enable analytical solutions of a system's dynamics. The more realistic structures, like small-world and stochastic block models, are not typically analytically solvable.

Deterministic vs. stochastic updating

The reliability of information transfer, $\beta \geq 0$, describes the accuracy of a node's perception of the beliefs of their neighbors. If you're familiar with statistical mechanics, $\beta$ behaves as an inverse "temperature" of the system: when $\beta$ is small, the reliability of information transfer is low (weakly held beliefs with random fluctuations, not easily observable social information, etc.).

$\beta$ is used while updating the state of an agent. If an agent can lower its energy at a given timestep ($\Delta \mathcal{H}_i < 0$), it does so with probability one. If changing its state raises its energy ($\Delta \mathcal{H}_i > 0$), it does so with probability $[1 + \exp(\beta \Delta \mathcal{H}_i)]^{-1}$